Jump to: 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 · 11 · 12 · 13 · 14 · 15 · 16
17 · 18 · 19 · 20 · 21 · 22 · 23 · 24 · 25 · 26 · 27 · 28 · 29 · 30 · 31 · 32


Golden Horagram #6
#30 of The Wilson Scale Tree

1/2—3/7, levels 0 and 3
(3Phi+1)÷(7Phi+2)
= 0.439291419
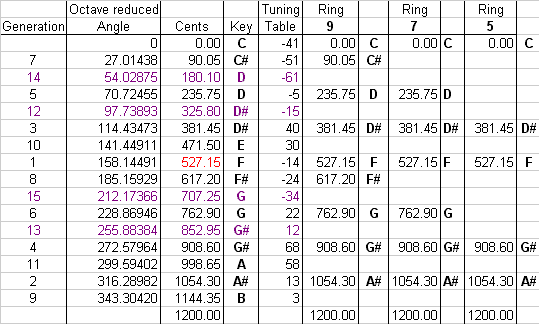
= generator angle 158.1449108°
= generator interval 527.15 cents

RingL size
(cents)		 s size
(cents)		RatioStep size
Order
5381.45 145.701+PhiLsLss
7235.75 145.70PhiLssLsss
9145.70 90.05PhisLLLsLLLL
1690.05 55.65PhiLLsLsLsLLsLsLsLs

Notes: Generator lies on a ridge of high harmonic entropy about half way between 4:3 and 11:8.

Consonant Ratio Approximated·Ring 5·Ring 7·Ring 9
7:5+0c @ 583c [10:7] 0 0 1
9:7+2c @ 437c [14:9] 0 1 3
5:4-5c @ 381c [8:5] 2 4 6
7:4-5c @ 964c [8:7] 0 2 4
11:6+5c @ 1054c = 2 generators [12:11] 3 5 7

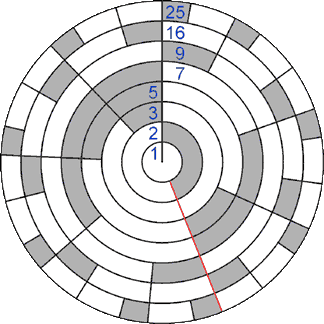
horagram

Mature rings: 3, 9 on out
tree route

Modes (in cents)

Ring 5
010i Alloyed - Interlaced - Immature - Improper
 
0 381 527 909 1054
0 146 527 673  819
0 381 527 673 1054
0 146 291 673  819
0 146 527 673 1054

  

Ring 7
110 Gold - Interlaced - Immature
 
0 236 381 527 763 909 1054
0 146 291 527 673 819  964
0 146 381 527 673 819 1054
0 236 381 527 673 909 1054
0 146 291 437 673 819  964
0 146 291 527 673 819 1054
0 146 381 527 673 909 1054

  

Ring 9
111 Gold - Interlaced - Mature
 
0  90 236 381 527 617 763 909 1054
0 146 291 437 527 673 819 964 1110
0 146 291 381 527 673 819 964 1054
0 146 236 381 527 673 819 909 1054
0  90 236 381 527 673 763 909 1054
0 146 291 437 583 673 819 964 1110
0 146 291 437 527 673 819 964 1054
0 146 291 381 527 673 819 909 1054
0 146 236 381 527 673 763 909 1054

data table

MIDI files
NYA

|   Horagram & Scale Menus  |   NEXT  |