· Prime Limit
· Octave Repeating3-prime-limit tuning is very ancient, and has been widespread at various times in many world cultures, including the West. It is known most widely now as Pythagorean tuning, after the Greek philosopher Pythagorus, who is often credited with promoting its use.
| Scale Degree | Gen- era- tion | 3^gen- eration | : | 2^x divisor | Quotient | Cents | Cents devia- tion from 12 EDO | Tun- ing Table | Round- ed Tuning Table | Note Name |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | : | 1 | 1 | 0.00 | 0.00 | -11 | C | |
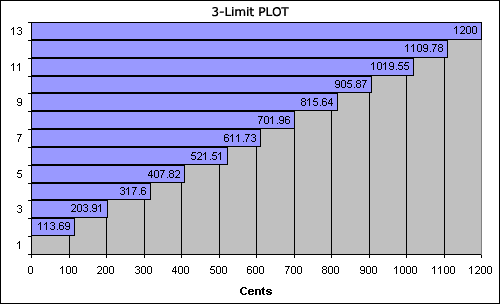
| 2 | 8 | 2187 | : | 2048 | 1.067871094 | 113.69 | 13.69 | 2.93 | 3 | C# |
| 3 | 3 | 9 | : | 8 | 1.125 | 203.91 | 3.91 | -6.84 | -7 | D |
| 4 | 10 | 19683 | : | 16384 | 1.20135498 | 317.60 | 17.60 | 6.84 | 7 | D# |
| 5 | 5 | 81 | : | 64 | 1.265625 | 407.82 | 7.82 | -2.93 | -3 | E |
| 6 | 12 | 177147 | : | 131072 | 1.351524353 | 521.51 | 21.51 | 10.75 | 11 | F |
| 7 | 7 | 729 | : | 512 | 1.423828125 | 611.73 | 11.73 | 0.98 | 1 | F# |
| 8 | 2 | 3 | : | 2 | 1.5 | 701.96 | 1.96 | -8.80 | -9 | G |
| 9 | 9 | 6561 | : | 4096 | 1.601806641 | 815.64 | 15.64 | 4.89 | 5 | G# |
| 10 | 4 | 27 | : | 16 | 1.6875 | 905.87 | 5.87 | -4.89 | -5 | A |
| 11 | 11 | 59049 | : | 32768 | 1.802032471 | 1019.55 | 19.55 | 8.80 | 9 | A# |
| 12 | 6 | 243 | : | 128 | 1.8984375 | 1109.78 | 9.78 | -0.98 | -1 | B |
Play Tuning
| Largest step size: | 113.69 c | (2187:2048) |
| Smallest step size: | 90.22 c | (256:243) |
| Number of step sizes: | 2 |
Very high odd limit: 177,147.
HC = 12.1
2004 by David J. Finnamore
tuning@elvenminstrel.com