Getting the Most Out of Pro Tools
Why Cutting Lows Can Cause Digital Clipping
Have you ever wondered why rolling off low frequencies can sometimes cause a waveform to clip? It seems like, since you're removing energy, and the volume is going down, that the peaks should be less. That's not always the case.
The two images below demonstrate how removing low frequencies can sometimes cause digital clipping. This is an idealized, controlled situation created strictly by mixing simple waveforms generated by the Pro Tools Signal Generator plug-in. That makes it easier to see what is happening than with a real-world example of rolling off lows from a complex waveform, and it eliminates the possibility that the clipping is caused by an EQ plug-in doing something it shouldn't. Three waveforms in three different frequency ranges are used:
- 30 Hz sine, steady state
- 150 Hz triangle, steady state
- 7 KHz sawtooth, positive-rectified, enveloped to form a transient
None of the waveforms alone clips.
Image 1: All three waveforms summed together - no clipping. The top three are the individual waveforms, the bottom one is the mix.
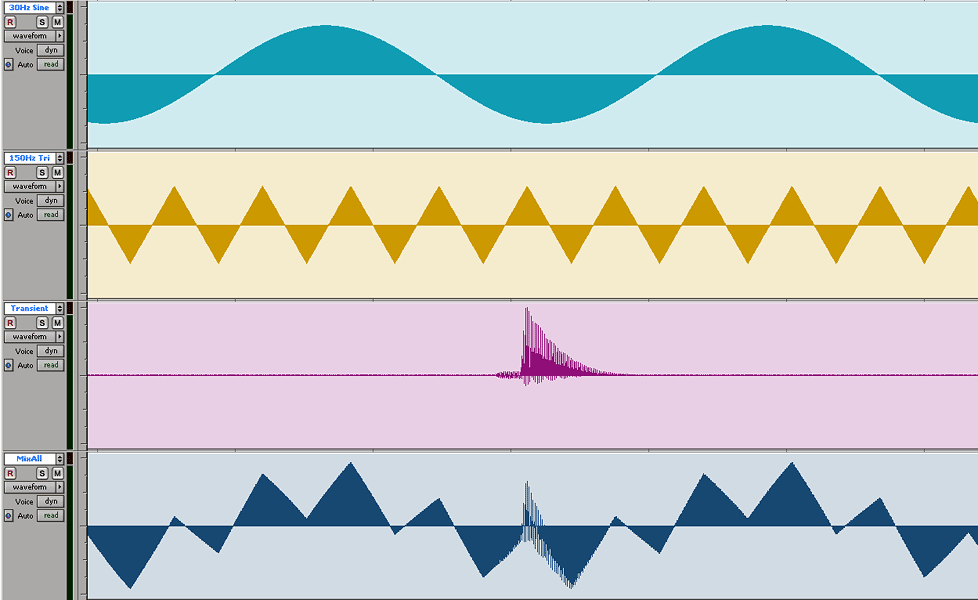
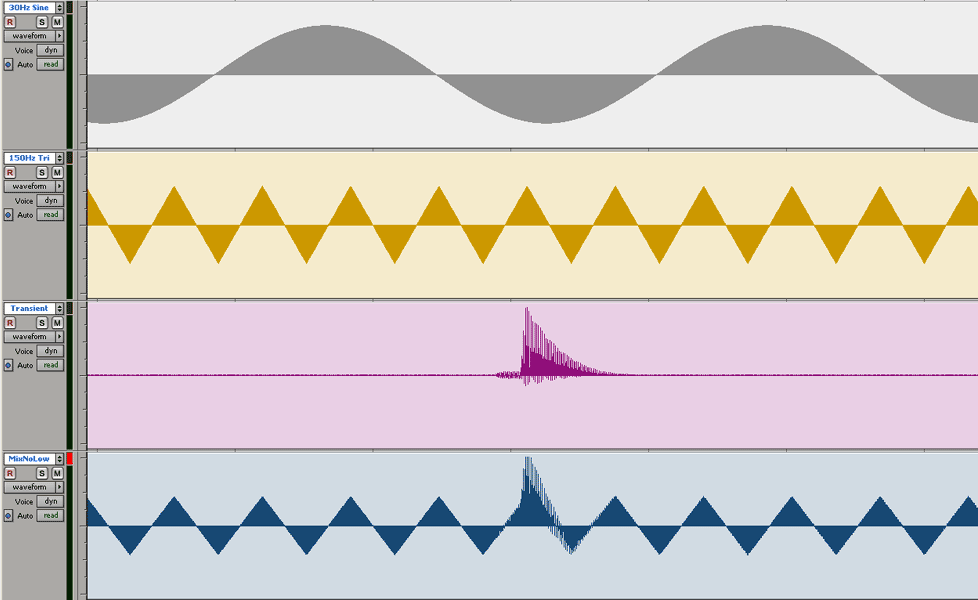
Image 2: 30 Hz sine muted, triangle and transient summed - the transient clips.
In the first image, notice how the triangle wave "rides" the sine wave. They modulate each other. The transient is also modulated by both the sine and triangle (and vice versa). The transient occurs during a negative excursion of the 30 Hz sine wave and a positive excursion of the triangle wave. The greater energy of the 30 Hz sine wave dominates, causing the transient to begin its rise from a point well below 0 volts. The summed triangle and transient waves exceed the positive range of the system (the room from 0 to maximum positive excursion). However, since their peaks occur during a negative excursion of the low sine wave, they don't clip.
In the second image, the transient, riding up on the positive peak of the triangle wave, exceeds the headroom of the system. It clips because it began its rise from a place well above 0 volts, on the back of the triangle wave, so to speak.
To reduce the math to simple terms, let's say the system can handle from -10 to +10. The 30 Hz sine wave travels from
DUC ID: daeron80
Written: May 2006
Copyright © 2006, all rights reserved
David's Personal Home Page