· Prime Limit
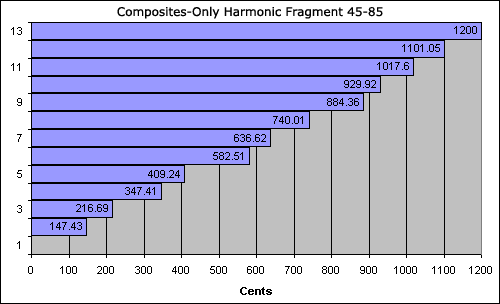
· Octave RepeatingWhatever the method of generation, in almost every set of tunings, one tuning stands out. This is the stand-out composites only harmonic fragment tuning. It's the first one to span less than an octave, and it has largest smallest step (if you follow me), and the least difference between largest and smallest step sizes. It's the first one to have a non-superparticular ratio as the smallest step. It also has lots of common tones.
| Scale Degree | Har- monic | Ratio | Quotient | Cents | Tuning Table | Rounded Tuning Table | Note Name |
|---|---|---|---|---|---|---|---|
| 1 | 45 | 1:1 | 1 | 0.00 | -34.40 | -34 | C |
| 2 | 49 | 49:45 | 1.088888889 | 147.43 | 13.03 | 13 | C# |
| 3 | 51 | 17:15 | 1.133333333 | 216.69 | -17.72 | -18 | D |
| 4 | 55 | 11:9 | 1.222222222 | 347.41 | 13.01 | 13 | D# |
| 5 | 57 | 19:15 | 1.266666667 | 409.24 | -25.16 | -25 | E |
| 6 | 63 | 7:5 | 1.4 | 582.51 | 48.11 | 48 | F |
| 7 | 65 | 13:9 | 1.444444444 | 636.62 | 2.22 | 2 | F# |
| 8 | 69 | 23:15 | 1.533333333 | 740.01 | 5.60 | 6 | G |
| 9 | 75 | 5:3 | 1.666666667 | 884.36 | 49.96 | 50 | G# |
| 10 | 77 | 77:45 | 1.711111111 | 929.92 | -4.48 | -4 | A |
| 11 | 81 | 9:5 | 1.8 | 1017.60 | -16.81 | -17 | A# |
| 12 | 85 | 17:9 | 1.888888889 | 1101.05 | -33.36 | -33 | B |
Play Tuning
| Largest step size: | 173.27 c | (21:19) |
| Smallest step size: | 45.56 c | (77:75) |
| Number of step sizes: | 12 | |
| Prime Limit: | 23 | |
| Odd Limit: | 77 | |
| HC = | 30.7 | |
2005 by David J. Finnamore
tuning@elvenminstrel.com