|
KEY & |
| David's Home Page | Tuning Pages Menu | Tuning Methods |
5- TO 9-TONE, OCTAVE-REPEATING SCALES
FROM WILSON'S GOLDEN HORAGRAMS OF THE SCALE TREE
David J. Finnamore
KEY
Example Page with Explanations
My original goal with these pages was to present the diagrams, tables, and other data in a convenient, one-page format to print and stick in a notebook. It turns out that there are just too many interesting and relevant facets of the Golden horagrams to always fit on a single page. Still, you should be able to print them directly from your browser and build a pretty useful reference document. For 8.5 X 11 inch paper, you'll need to set your margins to 0.5 inches (I guess that would be approx 22 X 28 cm paper with 1.25 cm margins in most of the world). Under Windows, I've had better luck with IE than with Netscape, overall. For some odd reason, Netscape ignores my margin settings and cuts off the right edges of the horagrams.
These conventions are observed on the horagram pages in the menu above:
- I have colored the generator red wherever feasible.
- Ring numbers, usually shown in blue, refer to the number of steps the ring is divided into, not how many rings it is from the center. For example, "Ring 7" does not necessarily mean the 7th ring from the center, it means the ring that contains a total of exactly 7 divisions, or scale degrees.
- In the table to the left of each horagram, the "Ratio" column shows the
L:svalue in terms of Phi. - Under each horagram are listed the Mature rings. See the Intro page for details.
- In the horagram itself, the large steps are white, the small ones are gray. I find that helps follow the divisions at a glance.
- I have not plotted as many rings of the horagrams as Wilson did, since I'm almost exclusively interested in octave repeating scales with 5 to 9 tones per octave.
- Only those rings are spelled out in all modes, and the Notes section only refers to intervals found in those rings unless otherwise stated.
- In the Notes section, I show which consonances are closely approximated.
- By "consonances" I mean complexity
(n*d) < 105- an arbitrary point, but seems to have the most widespread agreement (or at least the fewest objections) on the Tuning List. When I use the term "simple consonances," I mean those that can be reliably accurately tuned using harmonic timbres by tuning out the beats (that is, by ear). Most of those have a complexity less than about 53, but 11:8 and 13:8 are notable exceptions. - By "closely approximated" I mean within 7 cents. That's fairly tight but if you open the door much wider you end up with ungainly lists of approximations.
- At the end of each line, I show in brackets the inversion of the interval, even when its complexity exceeds 105. This, of course, is because both the simple interval and its inversion appear with equal frequency. (Sometimes the simpler of two intervals is in brackets. That just means I discovered the other one in the mode list first.)
- By "consonances" I mean complexity
- The term "generation(s)" is not inclusive of the 12 o'clock line. For example, for a generator of 100 cents, two generations, also referred to as generation 2, are 200 cents.
- In the table at the bottom of each horagram page
- The lines in purple are those that exceed 11 generations, and thus do not fit into a 12 note, octave-equivalent tuning table. That's important to me because my most often used synth has that restriction.
- The "Keys" listed are the keyboard keys the tones fall on in such a tuning table (usually nearest 12 EDO key), not necessarily how they should be spelled in notation.
- The Tuning Table values are offset to average near zero in the first 11 generations (plus C).
- Each MIDI/mp3 file example is, necessarily, only one small window on the scale and the tuning it exhibits. I don't pretend to have exhausted the resources of these scales; I've barely begun to explore them. But they should give you a taste of some of the sonic properties of each scale. They may not be the greatest music in the world but they have their Moments. [All together now: GROAN!]
There are three characteristics of each ring that I note. Whether it's
- Gold or alloyed
- Interlaced or GR
- Mature or Immature
There are eight possible logical permutations. All eight occur in 5- to 9- number rings of the first 16 Golden horagrams. Since each characteristic is a binary state, a ring may be labled 000, 001, 010, etc. to convey this information more succinctly. I associate 1 with Gold, interlaced, and mature; 0 with alloyed, GR, and immature. For instance, 101 indicates a ring that is Gold - GR - Mature.
I append an "i" to the three digit binary code when the scale is improper.
- Any scale of the Golden horagrams that is not improper is strictly proper. Only when
L:s= 2 can a single generator scale be proper-but-not-strictly-proper; and that condition cannot occur with a Noble generator. - A scale must have more than one small step to be improper.
- Step order and maturity have no bearing on propriety. Provided there is more than one
s, propriety is strictly a function of theL:sratio—ifL:s > 2, the scale will be improper. Thus, for any given interlaced Ring, the relationship of theL:sratio to Phi tells us the propriety of its scale.Ratio Quotient Propriety 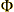
1.618 Proper (=>1)+ 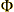
=>2.618 Improper 3- 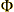
1.382 Proper 1+(1/(2+ 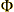 )
)
1.276 Proper 1+(1/(3+ 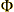 )
)
1.217 Proper 1+(1/(3- 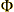 ))
))
1.724 Proper
As far as I can see, all the Golden horagramic scales are CS (constant structure). I can't see any way that an interval could occur more than once in these scales without being composed of the same set of steps.
LEXICON
| Term | Definition |
|---|---|
| Alloyed Ring | L:s does not equal Phi. However, all rings of the Golden Horagrams have some relationship to Phi. |
| Convergent Pair | A pair of intervals at the base of a path toward convergence on the scale tree. Represented on the scale tree as two fractions. Each fraction represents a unique MOS scale generator in the form of a certain number [numerator] of equal divisions [denominator] of an interval of equivalence. The formula for convergence uses the pair of fractions in conjunction with Phi. |
| Generator | The interval that is "stacked" or added onto itself over and over again to produce all of the intervals in a horagram. |
| Gold | Characterised by the Golden Ratio, Phi |
| Golden Ring | L:s = Phi |
| Golden/Noble Ratio | A ratio equal to or related to Phi. Sometimes "golden" is restricted to Phi, while "noble" refers to any number related to P\phi. |
| GR | Generator plus remainder. Describes rings of a horagram before the cumulative generations have exceeded 1200 cents; not an interlaced ring. |
| Horagram | A diagram made of concentric circles and radial lines, the angles of which define interval sizes. |
| Improper Scale | See Definitions of tuning terms. |
| Interlaced Ring | One which has more than one L and s each, distributed among each other. Not GR. |
| L:s | The ratio of the large interval size to the small interval size. |
| Level | As in "level 5"; or "levels 1 & 4." How many times the scale tree has branched at, and including, a given node. I count the 1/3 node as level 1. The tree splits into two branches at each node, so level 2 has two nodes, 1/4 and 2/5; level 3 has four nodes, level 4 has 8 nodes, and so on. See the scale tree. |
| Mature Ring | The large interval is equal in size to the previous ring's small interval. |
| MOS | Moment of Symmetry. Erv Wilson's term for scales with a single generator and exactly two interval sizes. All rings of the Golden horagrams are MOS. |
| Phi | The Golden number or relation, whose inversion is itself minus 1. Equal to (SQRT(5)+1)/2 |
| Ring Number | The number of intervals in a ring. |
| Ring of Convergence | The first Golden ring, going outward from the center of the horagram. All rings further out will also be Gold. Abbr. ROC. |
| ROC | Ring of Convergence. |
| Scale Tree | Erv Wilson's application of the Lambdoma to scale organization. |
| INTRO & EXPLANATION | MENUS | KEY & LEXICON | HEAR EXAMPLES |
| David's Home Page | Tuning Pages Menu | Tuning Methods |
Comments and corrections welcome: tuning@elvenminstrel.com