Golden Horagram #Number by closeness of the convergent pairs to the root of the tree
#Wilson's number of
The Wilson Scale Tree
Convergent pair of ET generators, and their levels of the scale tree
| = Generator Quotient |
| = generator angle Generator Angle° |
| = generator interval Generator Interval in cents |
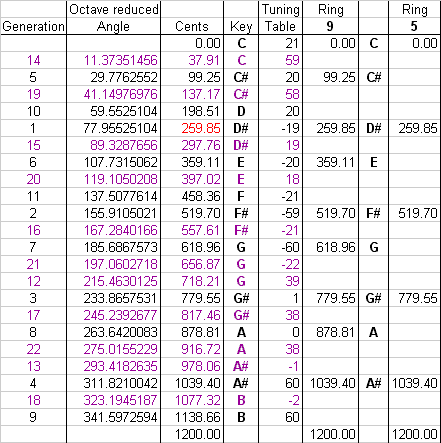
Table of scale properties
| Ring | L size (cents) |
s size (cents) | Ratio | Step size Order |
|---|---|---|---|---|
| 5 | 259.85 | 160.60 |  | LLLLs |
| 9 | 160.60 | 99.25 | | sLsLsLsLL |
| 14 | 99.25 | 61.34 | | LLsLLsLLsLLsLs |
| 23 | 61.34 | 37.91 | | sLsLLsLsLLsLsLLsLsLLsLL |
Notes: Converges on gold very early, at ring 4.
Table of consonant ratios approximated · how many instances of each in each scale
| · | · | ||||
| 13:8 | +0c @ 841c [16:13] | 0 | 3 | ||
| 10:7 | +1c @ 619c [7:5] | 0 | 2 | ||
| 11:7 | -3c @ 780c = 3 generations [14:11] | 2 | 6 | ||
| 5:3 | -6c @ 879c [6:5] | 0 | 1 | ||
| 7:6 | -7c @ 260c = generator [12:7] | 4 | 8 | ||
Horagram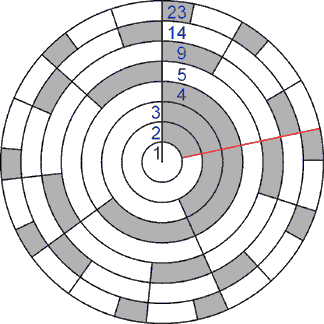
Mature rings: which rings of this horagram are mature
Route of generator up scale tree—gold dot shows point of convergence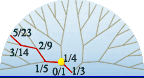
| Modes of the scales (in cents) | ||
|---|---|---|
Ring 5
0 260 520 780 940 0 260 520 680 940 0 260 420 680 940 0 161 420 680 940 |
Ring 9
0 161 260 420 520 680 780 940 1101 0 99 260 359 520 619 780 940 1039 0 161 260 420 520 680 841 940 1101 0 99 260 359 520 680 780 940 1039 0 161 260 420 581 680 841 940 1101 0 99 260 420 520 680 780 940 1039 0 161 321 420 581 680 841 940 1101 0 161 260 420 520 680 780 940 1039 |
|
MIDI files
MP3 files
| Horagram & Scale Menus | NEXT |